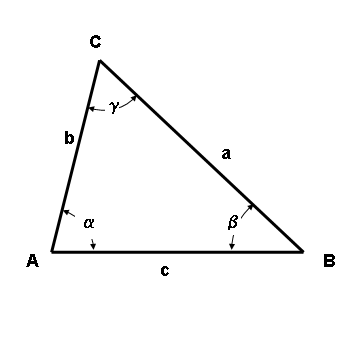
De Kosinussatz stellt i de Trigonometrii vo dr Ebeni e Beziehig zwüsched de Siite vomene Drüeck und em Kosinus vo eim vo de Winkel her.
Für di drü Siite a , b und c vomene Drüeck sowie em Winkel gegenüber vo de unbekannte Siite gilted:
Bezeichnungen im Dreieck
a
2
=
b
2
+
c
2
−
2
b
c
cos
α
{\displaystyle a^{2}=b^{2}+c^{2}-2\,b\,c\,\cos \alpha }
b
2
=
a
2
+
c
2
−
2
a
c
cos
β
{\displaystyle b^{2}=a^{2}+c^{2}-2\,a\,c\,\cos \beta }
c
2
=
a
2
+
b
2
−
2
a
b
cos
γ
{\displaystyle c^{2}=a^{2}+b^{2}-2\,a\,b\,\cos \gamma }
Us em Kosinussatz chammer unter anderem au de Satz vom Pythagoras forme, wenn de Winkel
γ
=
90
∘
{\displaystyle \gamma =90^{\circ }}
c
2
=
a
2
+
b
2
−
2
⋅
a
⋅
b
⋅
0
→
c
2
=
a
2
+
b
2
{\displaystyle c^{2}=a^{2}+b^{2}-2\cdot a\cdot b\cdot 0\rightarrow c^{2}=a^{2}+b^{2}}
Di folgende Zahle sind grobi Nöherige. Geh seg es Drüeck ABC, wo alli drü Siite vorgeh sind.
a
=
5
c
m
{\displaystyle a=5\;{\rm {cm}}}
b
=
4
c
m
{\displaystyle b=4\;{\rm {cm}}}
c
=
4
,
5
c
m
{\displaystyle c=4{,}5\;{\rm {cm}}}
Gsuecht isch de Winkel
β
{\displaystyle \beta }
b
2
=
a
2
+
c
2
−
2
⋅
a
⋅
c
⋅
cos
β
{\displaystyle b^{2}=a^{2}+c^{2}-2\cdot a\cdot c\cdot \cos \beta }
2
⋅
a
⋅
c
⋅
cos
β
=
a
2
+
c
2
−
b
2
{\displaystyle 2\cdot a\cdot c\cdot \cos \beta =a^{2}+c^{2}-b^{2}}
cos
β
=
a
2
+
c
2
−
b
2
2
⋅
a
⋅
c
=
(
5
c
m
)
2
+
(
4
c
m
)
2
−
(
4.5
c
m
)
2
2
⋅
5
c
m
⋅
4.5
c
m
=
0
,
46
{\displaystyle \cos \beta \,=\,{\frac {a^{2}+c^{2}-b^{2}}{2\cdot a\cdot c}}={\frac {(5\,{\rm {cm}})^{2}+(4\,{\rm {cm}})^{2}-(4.5\,{\rm {cm}})^{2}}{2\cdot 5\,{\rm {cm}}\cdot 4.5\,{\rm {cm}}}}=0{,}46}
β
=
arccos
0
,
46
=
62
,
5
∘
_
{\displaystyle \beta =\arccos \,0{,}46={\underline {62{,}5^{\circ }}}}