D Püramide in dr Geometrii

D Püramide isch e (dreidimensionale) Körper in dr Geometrii. Es isch e Polyeder, wo us meerere ebene Flechene bestoot, wo anenander lige, und vo deene isch äini e Polygon und alli andere si Dreiegg. Die Dreiegg (Siteflechene) bilde d Mantelflechi.

E Püramide mit em Spitz (änglisch apex) oobe und dr Grundflechi (änglisch base) unde

Konstrukzioon

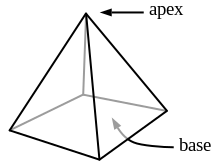
Vom ene Punkt, em Spitz vo dr Püramide, goot e Büschel vo Straale us, wo alli Straale von em en Ebeni schniide. Die Schnittpünkt si d Eggepünkt vo dr Grundflechi vo dr Püramide. Mä cha d Konstrukzioon au mit irgend ere Grundflechi afoo, won es Vilegg (Polygon) in ere Ebeni isch, und mit eme Punkt usserhalb vo deere Ebeni, wo denn dr Spitz vo dr Püramide wird. Wemm mä jeede Eggepunkt vo dr Grundflechi mit em Spitz verbindet, entstoot s erwäänte Straalebüschel. D Pünkt vo jeder äinzelne Grundflechekante si über d Dreieggflechi mit em Spitz vo dr Püramide verbunde. Eso erfüllt d Püramide au d Definizioon vom ene Chäigel.

Äigeschafte

Wenn d Grundflechi von ere Püramide n Egge het, so isch d Zaal vo de (dreieggige) Siteflechene au gliich n. Zämme mit dr Grundflechi het d Püramide denn im Ganze n+1 Flechene. D Zaal vo de Egge isch au gliich n+1, nämlig n Eggen vo dr Grundflechi und dr Spitz. D Grundflechi het n Kante und d Sitelinie vom Straalebüschel, wo d Egge vo dr Grundflechi mit em Spitz vo dr Püramide verbinde, si genau so vil, das macht im Ganze 2n Kante. Eso isch dr eulerschi Polyedersatz über d Zaale vo Egge (e), Flechene (f) und Kante (k) erfüllt:

$e+f=(n+1)+(n+1)=2n+2=k+2.$

Für d Berächnig vom Volume von ere Püramide isch dr Begriff vo dr Hööchi wichdig. Mä verstoot drunder dr (chürzist) Abstand vom Spitz zu dr Ebeni, wo d Grundflechi din ligt.

D Berächnig vom Voluume

D Formle

S Voluume V von ere Püramide wird us em Inhalt vo dr Grundflechi (G) und dr Hööchi (h) berächnet

$V={\frac {1}{3}}\cdot G\cdot h$

Die Formle gältet für alli Püramide. Es schbiilt also käi Rolle, öb d Grundflechi e Dreiegg, Vieregg, Fümfegg, ... isch. D Formle isch au gültig, wenn dr Fuesspunkt vo dr Hööchi nit dr gliich isch wie dr Middelpunkt vo dr Grundflechi oder d Grundflechi gar käi Middelpunkt het. Im Spezialfall von ere kwadratische Püramide bechunnt mä $V={\frac {1}{3}}\cdot a^{2}\cdot h$, wo a d Lengi vo dr Site vo dr Grundflechi isch und h d Hööchi. Die allgemäini Formle $V={\frac {1}{3}}\cdot G\cdot h$ entspricht übrigens dr Volumeformle $V={\frac {1}{3}}\cdot r^{2}\cdot \pi \cdot h$ für e Kräischäigel. Das lit dodra, dass jeedi Püramide d Definizioon vom ene allgemäine Chäigel erfüllt.

Weblingg

• Pyramide uf Mathworld (ängl.)

Dä Artikel basiert uff ere fräie Übersetzig vum Artikel „Pyramide_(Geometrie)“ vu de dütsche Wikipedia. E Liste vu de Autore un Versione isch do z finde.